
FFT size, window and transform overlap (interleave factor)The output from step 1 is complex data (32 bit integers) with a sampling frequency of 22kHz. To get a reasonable suppression of strong signals a window function has to be used.The purpose of the fourier transforms is to use them in a back transformation to restore the signal as a function of time - but without the frequencies disturbed by local amateurs. To restore the original signal one has to divide the back transformed data with the window function. This will create useless data zero divided by zero at the beginning and end of each transform. (A window function is always zero at the ends). Consequently the fourier transforms have to overlap so the useless data becomes superfluous. The restoration of the time function becomes particularly simple with a sine squared window in combination with an interleave factor of two. Therefore the first conversion from the time domain to the frequency domain is done this way. The transform is taken in 1024 points giving a bandwidth of about 30Hz. Because of the dynamic range required it is not possible to use MMX instructions since they allow only 16bit. The Pentium is quite a bit faster with floating point arithmethics compared to 32 bit integer arithmetics so the first FFT is done with floating point instructions. The code is written in C and placed in RXSUB1.C The code is optimised for the Watcom C compiler, I have optimised the instruction sequencing (and made the code somewhat less transparent) in order to get the highest possible speed. The fft routine has an extra "butterfly loop" to remove the alias signal due to the conversion from real to complex data. The alias signal is -50dB close to the edges and -80dB or below over the main part of the 20.3kHz wide processed spectrum. The last step of the fft routine is a multiplication with a correction function. This correction function is determined during the noise blanker initialisation and it corrects for amplitude and phase errors in the hardware. As a result the frequency response of the PC receiver is extremely flat with absolutely linear phase response. The fft routine produces complex amplitudes, power spectra and averaged power spectra as output. The average power spectrum, summed over the two channels (both polarisations) and summed over 8 transforms (0.18 seconds) is stored in the array limiter_avgpwr[]. Every 0.18 seconds the average power spectrum is averaged once more in a leaky integrator (RC time constant) to form the array slow_spectrum which is the data used in the 100dB unpolarised power spectrum. The 100dB power spectrum constitutes a spectrum analyser with about 30Hz resolution bandwidth and with a 1Hz video filter. Performance - Timing and dynamic rangeWith a 200MHz Pentium and a SB16 sound card the performance is surprisingly good. The total CPU time consumption for the calculation of the first FFT, including the DMA operation for the sound board and the real to complex data transformation is about 15%, leaving about 85% of the total processing power to the succeding stages. This is the time used for the two channels in stereo.The images below show what the display looks like with very weak and with very strong signals. Under normal operation I place the noise floor at +20dB to get rid of all internal spurs and to ensure that the mast mounted preamplifiers produce all visible/audiable system noise. The dynamic range then is about 80dB which is usually enough at my location. (This is in 30Hz bandwidth, so it corresponds to 60dB in SSB bandwidth) In case the system becomes overloaded - and when it is not possible to tune for the interfering station to come outside the crystal filters, it is possible to insert up to 20dB attenuation in the signal path without any dramatic loss of S/N. There would be some extra spurs, both internal and due to harmonic distorsion as can be seen from the figures below. |

|
|
Fig 1. Pentium MMX 230MHz, TX chip set. Nothing connected to the Soundblaster input.
|

|
|
Fig 2. Pentium MMX 200MHz, HX chip set. Nothing connected to the Soundblaster input.
|
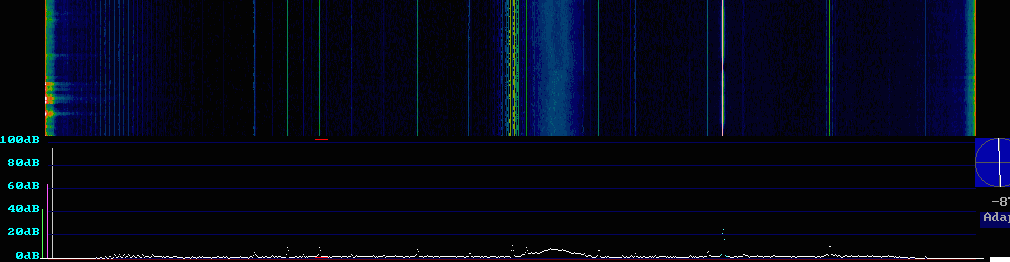
|
|
Fig 3. Pentium MMX 230MHz, TX chip set. Stereo receiver connected, but
mast mounted preamplifiers switched off.
|

|
|
Fig 4. Pentium MMX 230MHz, TX chip set. Stereo receiver connected, but
mast mounted preamplifiers switched off. The receiver is slowly tuned
about 2kHz with a very strong (+100dB) signal added.
|

|
|
Fig 5. Pentium MMX 230MHz, TX chip set. Stereo receiver connected and
mast mounted preamplifiers switched on. The lower part of the false colour
graph shows the noise floor with a dummy load replacing the antenna.
The internal spurs that dominate when no signal is connected to the Soundblaster differ slightly between different computers as can be seen from figure 1 and figure 2. The wide spurs, one in each channel are smeared out when a signal is connected The frequencies of the wide spurs are strongly depending of the computer temperature. When the noise floor is placed about 95dB below the saturation level, 15dB below the normal position for the noise floor, a strong signal placed at a low audio frequency causes several false responses. The lower part of figure 4 shows a signal at an audio frequency of about 3.5kHz produced with the mast mounted preamplifiers switched off, and with an oscillator at 144MHz added in the signal path. The following spectral lines are visible: Main signal (3.5kHz) 100dB Second harmonic (7kHz) 40dB Third harmonic (10.5kHz) 35dB Fourth harmonic (14kHz) 25dB Fifth harmonic (17.5kHz) 20dB Alias signal (22-3.5kHz) 20dBThe upper part of fig 4 shows how the spurs of different order move when the receiver is tuned slowly over a 2kHz range, moving the main signal from 1.5 to 3.5 kHz. The harmonics do not change amplitude much, but the alias signal drops rapidly as it moves inwards from the edge. Phase noise and some hum modulation is visible on the main signal. These components are not present when a good audio oscillator is fed to the PC. (My audio oscillator has too much harmonic distorsion to be useful here to demonstrate performance.) I do not know if the harmonic distorsion is produced in the Soundblaster or if it is produced in the radio hardware. If very strong signals are placed outside the 1 to 5 kHz audio range all false responses except the second and third harmonics disappear. It is easy to make sure they do not interfere with the desired signal. As can be seen from figure 3 the radio hardware has some hum due to overtones of the mains frequency that degrade performance at the low frequency side. The wide internal spur of the Soundblaster dominates the noise over a 2kHz region close to the center, but over most of the frequency range weak signals can be received at nearly full sensitivity even if a strong signal (95dB above noise) is present in the passband. When the noise floor is placed at the normal level at 20dB, the internal spurs are hidden in the noise as can be seen in fig 5. The only structure visible is the broad group of lines at the center. These lines are caused by loss of information due to the use of 16 bit arithmetics in the MMX when the signal is converted back to the time domain. This structure at frequency zero in the complex FFT (corresponding to an audio frequency of 11kHz) is clearly visible in figure 1 and 2. Note that it is a group with many lines in the false colour graph but that it is a single line in the spectrum display at the bottom. When the antenna is connected there is usually a large number of signals visible on the screen. They are produced by computers and hidden microprocessors in the neighbourhood. The gain is high for the false colour graps in fig 5. Signals well below the noise are visible, but the internal spurs of the Soundblaster 10dB below the noise are not visible. To SM 5 BSZ Main Page |