Bandwidth and sensitivity

Amateurs wanting to communicate over difficult propagation paths may use bandwidths of 1Hz and below. The very high sensitivity for sine waves one gets at narrow bandwidths will not only make it possible to find the desired signal. There is also a very large number of undesired signals originating in spurious emissions from computers and many modern "toys" that contain a chrystal oscillator and some silicon.

The high sensitivity also calls for the use of very high quality oscillators. Strong signals on other frequencies may have spurious emissions that normally would not be a problem because the receiver front end amplifiers and/or mixers will saturate before they are heard. The increased sensitivity associated with narrow filters makes it desireable to suppress spurs far better than what is usually done.

The ability to locate weak sinewaves over a wide frequency range that this page demonstrates is useful for finding the carrier of normal CW transmissions. This is a very good tool for finding signals reflected via the moon on VHF frequencies.

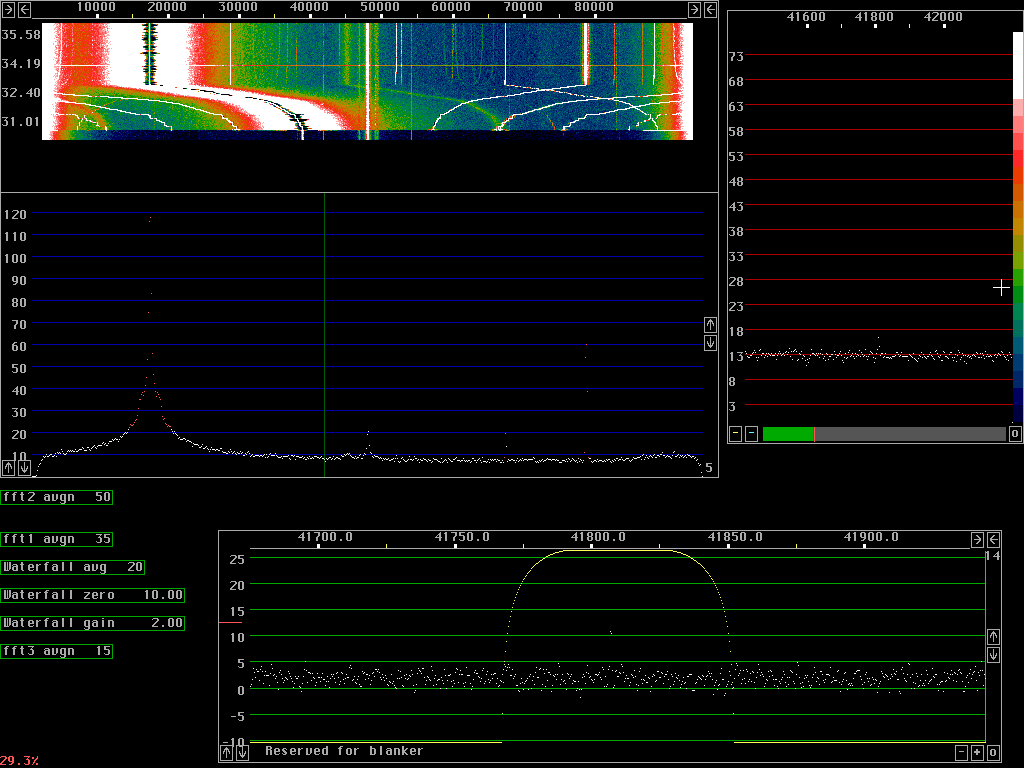
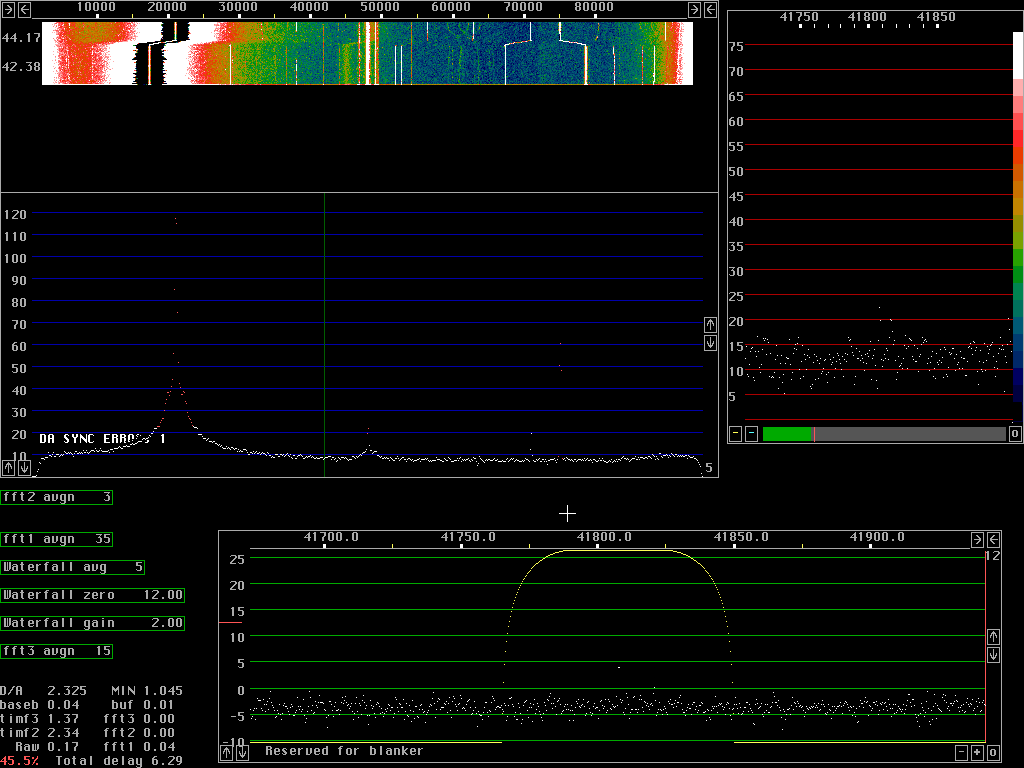
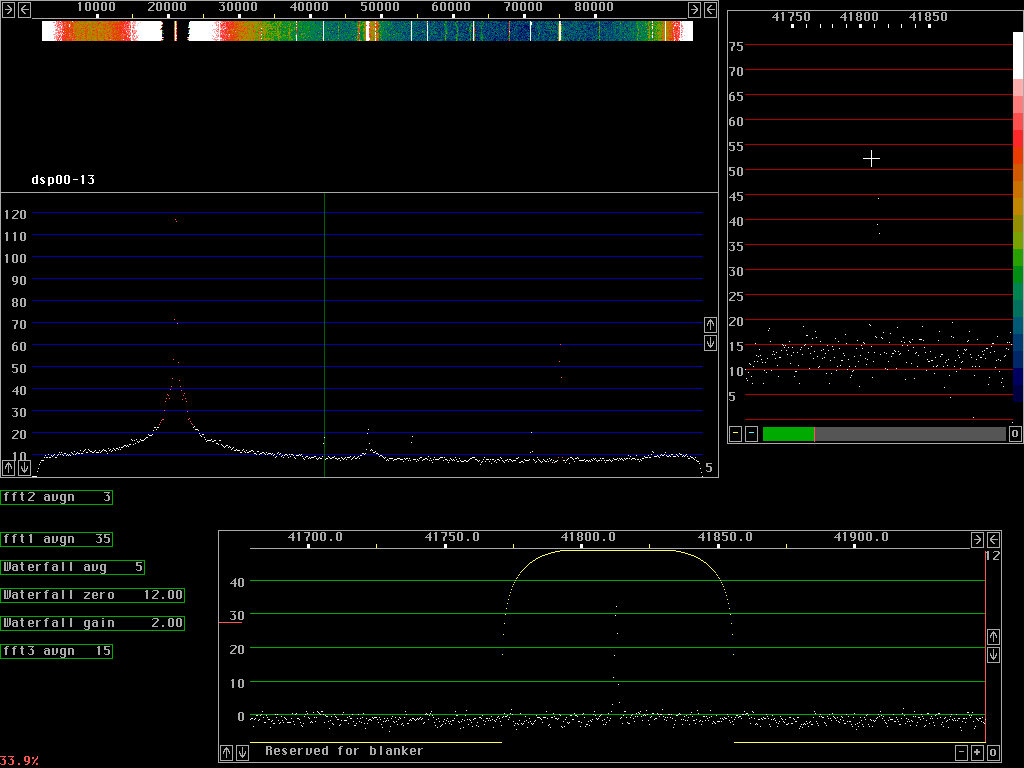
Two tone test showing spurs and sensitivity

After stopping at a fixed frequency the main signal is at 17.5kHz or +/- 30.5kHz audio. The unbalance spur which is also at +/- 30.5kHz audio shows up at 78.5kHz. The unbalance spur is suppressed by about 60dB in this case. The second order distorsion of the I/Q mixer and the audio amplifiers and possibly the Delta 44 itself comes at +/-70kHz audio It is equally strong as the corresponding unbalance spur, both are outside the waterfall, they are about 60 dB below the main signal. Third order and fourth order distorsion is also visible.

The spur at 67.5kHz is due to the 50kHz reference of the syntethiser used as local oscillator at 7.050MHz. It is a sideband about 90dB below the local oscillator. The 50kHz sideband is present on both sides of the local oscillator. The phase and amplitude relation is different in the I and Q channels compared to the main signal so the 50kHz spur to the unbalance spur is well visible at 28.5kHz

The desired signal is at 6.2kHz. It is a high quality tone generator and the signal is injected through a 100 ohm resistor to the chassis of the radio hardware. The very weak signal is easily seen at the bottom of the waterfall graph, before the cable to the signal generator was connected.

The audio signal at 6.2kHz has the same phase and amplitude in both I and Q so it appears with the same amplitude at 41.8 and 54.2kHz. The signal is clearly seen together with several weak spurs of unknown origin. Note that the 6.2kHz signal is a attenuated in the middle of the graph of fig.1.

Fig. 1. was recorded with 32768 point fft's for the waterfall graph using about 30% of the available processing power of the 650MHz PentiumIII.

As a comparison fig. 2 shows the same signals with 4 times larger fft's, 131072 points for the waterfall graph. Note that the 6.2kHz signal is much better visible compared to the upper part of fig.1.

Fig.3. Has the same level of the 7MHz signal as figures 1 and 2 but the 6.2kHz signal is increased by about 25dB. It is 100dB below the 7MHz signal here so it is 125dB below it in fig. 1 and fig.2.

The "high resolution graph" to the right of the waterfall graph shows the averaged spectrum used for the waterfall with a scale expanded to one pixel per fft bin. The weak signal is well visible - but the integration time is long.....

The "baseband graph" has the same resolution in all thre figures. It corresponds to 262144 points for the 96kHz sampling speed although it does not cover the full frequency range. It uses a sine squared window and the bandwidth is about 0.5Hz