
Fig 1.A sin3 window gives a dynamic range of 100 dB when the timf3 sampling rate is 15625 Hz.
|
The screen dumps on this page are all generated with the internal
signal generator of Linrad at a sampling rate of 1 MHz and with
an fft1 size of 8192.
The corresponding bandwidth is in the order of 300 Hz,
a little different depending on which window function is in use.
Figure 1 shows the screen for parameters that would be typical for earlier Linrad versions, a sin3 window with a timf3 sampling rate of 15625 Hz. |

Fig 1.A sin3 window gives a dynamic range of 100 dB when the timf3 sampling rate is 15625 Hz. |
|
In figure 1 the fixed frequency signal which is 100 dB below the
sweeping signal is keyed at an interval of 10.7 pixels in the
baseband graph.
The sweep period is 170 pixels with a sweep width of 125 kHz so
the frequency sweeps 7.85 kHz for one period of the keying of
the weak signal.
The signal characteristics are the same for all screen dumps on this
page.
As can be seen in the S-meter graph, the worst spurs, -100dB
below the strong signal are about 0.5 keying intervals away from
the passband which means they are about 4 kHz away from the desired
signal.
With the current state of the art
Real life dynamic range of modern amateur transceivers
better performance than that demonstrated in figure 1 is not needed,
but modern digital transmitters should easily be able to produce
significantly cleaner signals in the near future.
|
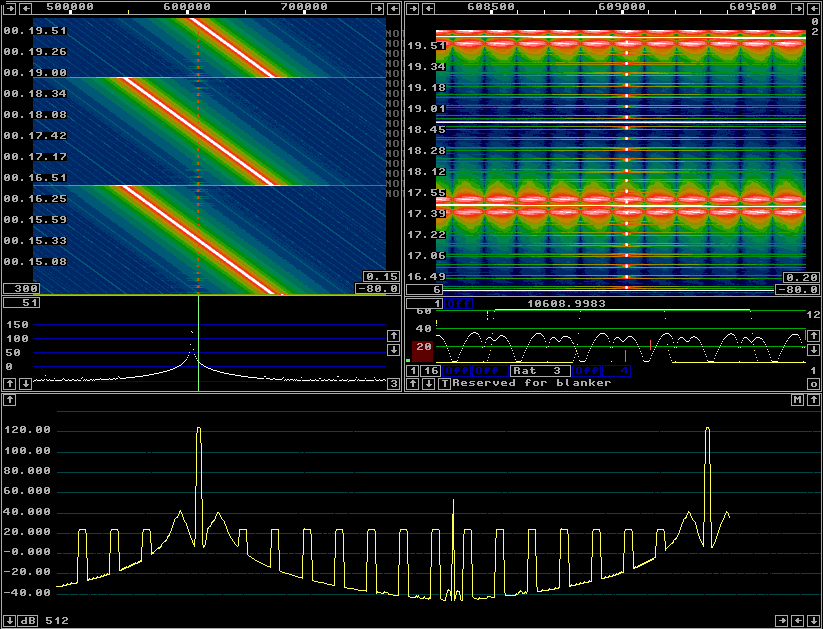
Fig 2.A sin2 window gives a dynamic range of 80 dB when the timf3 sampling rate is 15625 Hz. |
|
With a sin2 window the dynamic range is about 20 dB worse
as compared to a sin3 window as can be seen from figure 2.
The timf3 sampling speed is 15625 Hz in both figures.
The sin2 window requires less CPU time than the sin3 one. At a timf3 sampling rate of 31250 Hz the dynamic range is 105 dB with the sin2 window. The spurs are generated at twice the frequency separation and could become the limiting factor under some circumstances. Adequate dynamic range with a sine2 window might require a longer time span for fft1. |
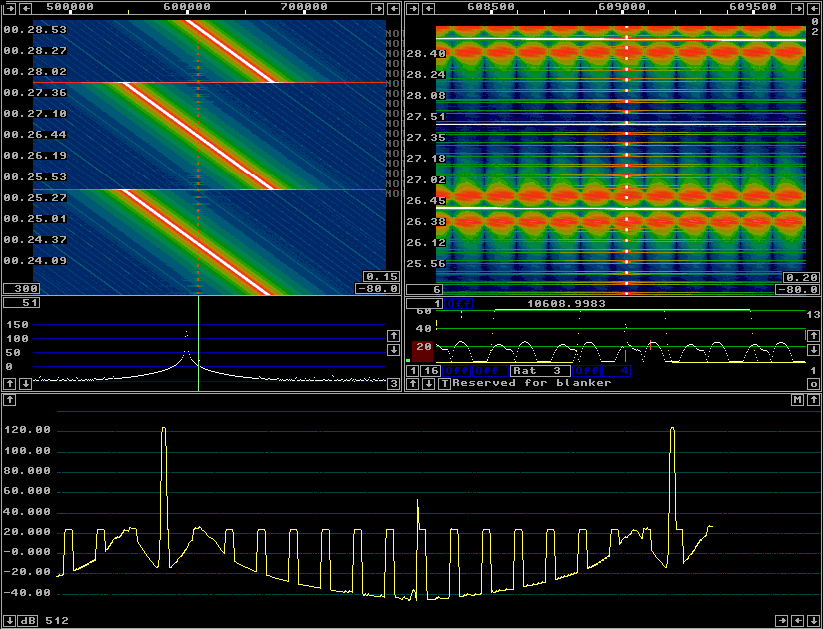
Fig 3.A sin2 window gives a dynamic range of 100 dB when the timf3 sampling rate is 31250 Hz. |
|
The error function erf(x) is a much better window than sinN
windows when the objective is good dynamic range with a short time
delay and with a large reduction in sampling rate.
Figure 4 shows that the dynamic range is about 150 dB with the erf(x) window at a timf3 rate of 15625 Hz. As compared to 85 dB for sin2 or 100 dB for sin3 this is very much better. |

Fig 4.A erf(x) window gives a dynamic range of 150 dB when the timf3 sampling rate is 15625 Hz. |
|
The dynamic range of 150 dB in the first mixer step in Linrad that can be seen in figure 4 is not really true.
Rounding errors due to the 24 bit precision of the floating point
arithmetics of the fourier transform itself creates spurs about 140 dB
below the strong signal.
It is obvious that 15625 Hz is higher than necessary for a good
dynamic range with the erf(x) window.
Figure 5 shows the performance with the erfc(x) window when the timf3 sampling rate is 7812.5 Hz. 140 dB at 2 kHz, falling rapidly at larger frequency separations is surely better than needed. |
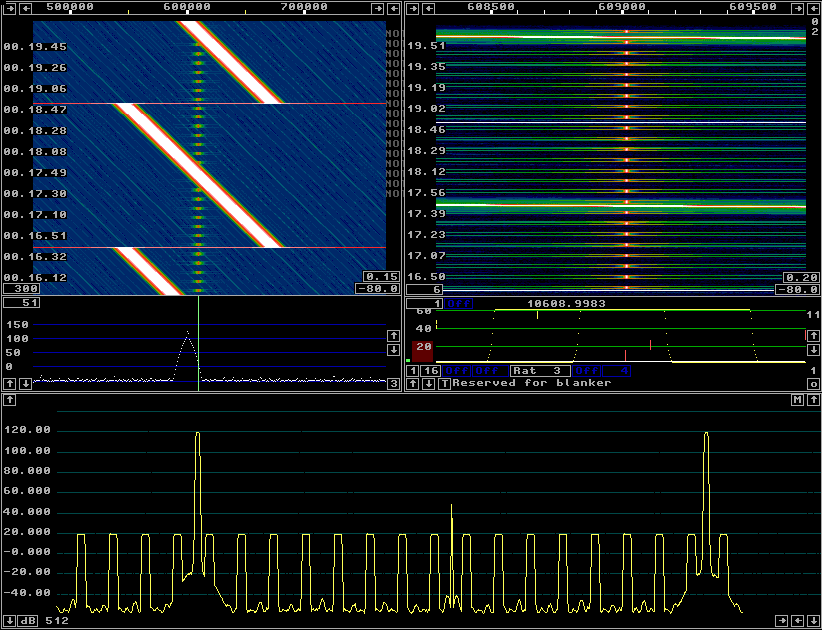
Fig 5.A erf(x) window gives a dynamic range of 140 dB when the timf3 sampling rate is 7812.5 Hz. |
|
By reducing the timf3 sampling rate by another factor of two to
3906.25 Hz the spurs related to the resampling process increase
in amplitude while moving closer to the passband.
80 dB at 1 kHz and 100 dB at 2 kHz as can be seen in figure 5 should
be perfectly adequate in real life situations.
On the other hand there is no reason to go this low in timf3
sampling speed.
|
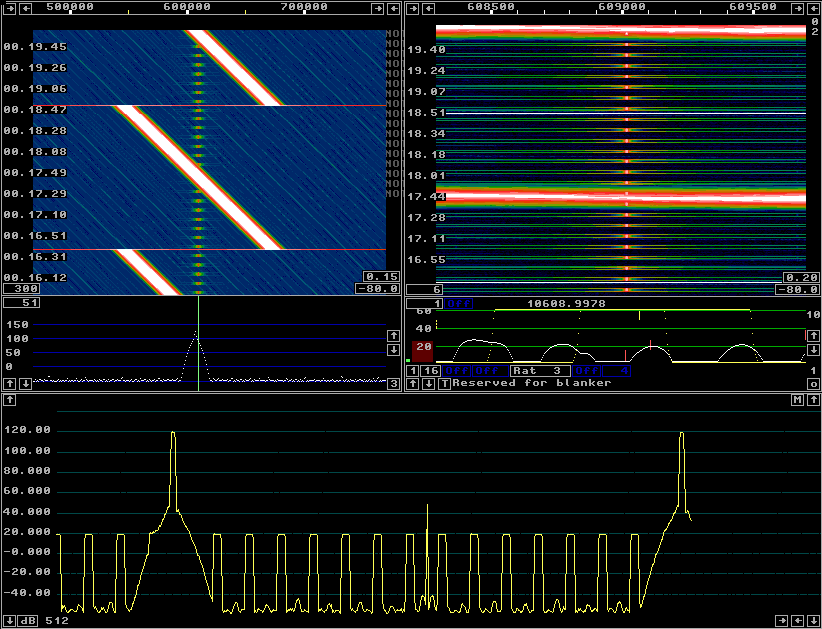
Fig 6.A erf(x) window gives a dynamic range of 80 dB when the timf3 sampling rate is 3906.25 Hz. The resampling spurs are at very close frequency separations and fall off rapidly at increasing separations. |
|
To SM 5 BSZ Main Page |