SM 5 BSZ - Linux dsp radio, the high resolution waterfall graph
(Feb 04 2001)

Searching for weak signals over a wide frequency range

With typical parameters for a moon-bounce radio covering 90kHz the number of fft bins are in the range 32768 to 524288 which means bandwidths in the range 6Hz to 0.2Hz assuming sin squared window functions. With a 1024 x 768 screen one would have 32 to 512 fft bins for each pixel.

The easiest strategy is to pick the largest power level out of the 32 to 512 values for each pixel. This will probably be sufficient because signals that would need a more clever search are probably too weak to be decoded anyway. It will be possible to dig deeper into the noise and present better indications for the presence of a signal on the waterfall graph but other things seem more interesting right now.....

Polarisation

Contrary to galactic noise, signals always have a polarisation. It means that one can combine the two signals from a X-yagi in such a way that one channel contains all the signal and 50% of the total noise while the other channel contains noise only.

If knowledge about the polarisation was available beforehand it would be better to reject the channel with noise only and search for signals in the correct polarisation only. A 3dB improvement!

Not knowing the polarisation one could display the summed power of the two channels using integration (summing several power spectra) to improve S/N. When summing spectra it is useful to calculate channel correllations and integrate them too. Over a long time the channel correllation integrates to zero if no signal is present or if the signal is present in one channel only, but if the polarisation is somewhere in between the correllation integrates to a nonzero value.

Taking the correllation into account compensates more or less for the fact that a square law detector looses more than 3dB S/N when the input signal drops by 3 dB when input S/N is very low. This way the sensitivity is relatively independent on polarisation and a signal that is present 3dB down in both channels becomes equally well visible as a signal that is present in one channel only.

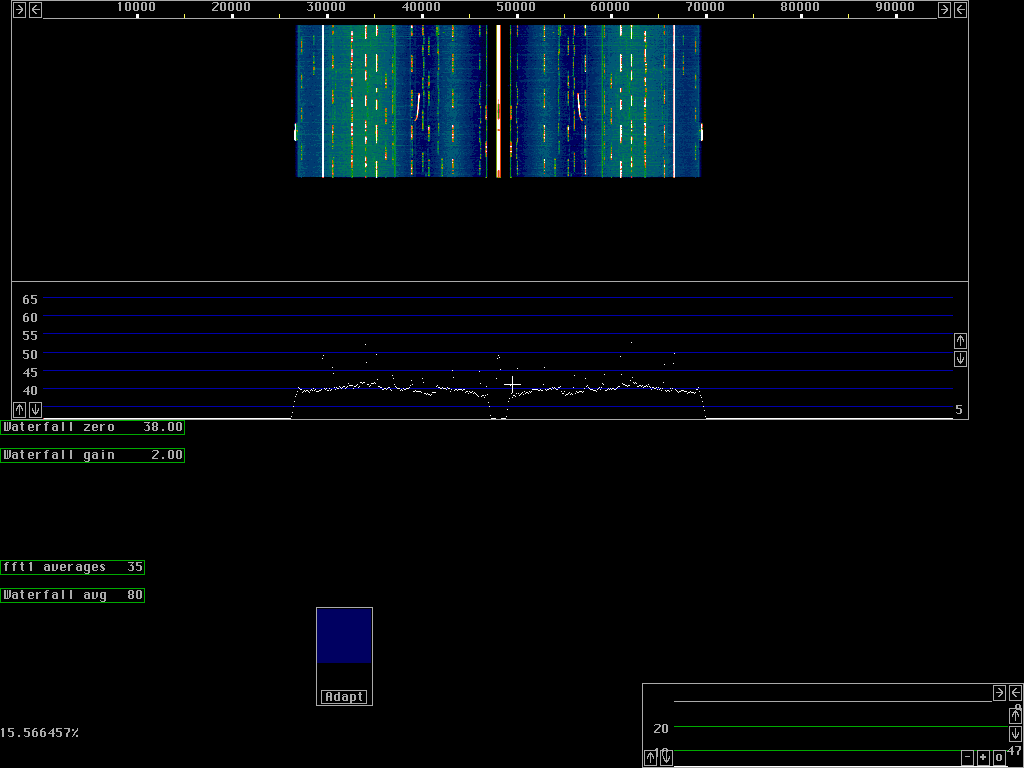
The simple waterfall graph

The first fft produces a full dynamic range spectrum using floating point arithmetics. This spectrum can be used for the waterfall graph by deselecting the second fft (and the wideband noise blanker). For 90kHz bandwidth the first fft is typically in the range 2048 to 16384 corresponding to about 12 to 100Hz bandwidth. The first fft bandwidth affects dynamic range and if no very strong signals are present near the desired frequency there is no need for high resolution.

Fig 1 shows a sequence from the Italian EME contest Okt 09 1999 at 0900-0908 UTC. The center frequency is 144.025MHz. The first fft is run with 8192 points and the screen is set up for 90kHz bandwidth.

The signal from the DAT recorder covers only 20kHz.

Since the Linux radio expects both an I and a Q signal but Q is zero for each channel, the 20 kHz passband is received twice at frequencies symmetrically around 48 kHz.


Fig 1. Waterfall power spectrum from the first fft. Effective resolution is 90Hz because this graph just sums the power for all points behind each pixel.

15% of the available CPU time is used.

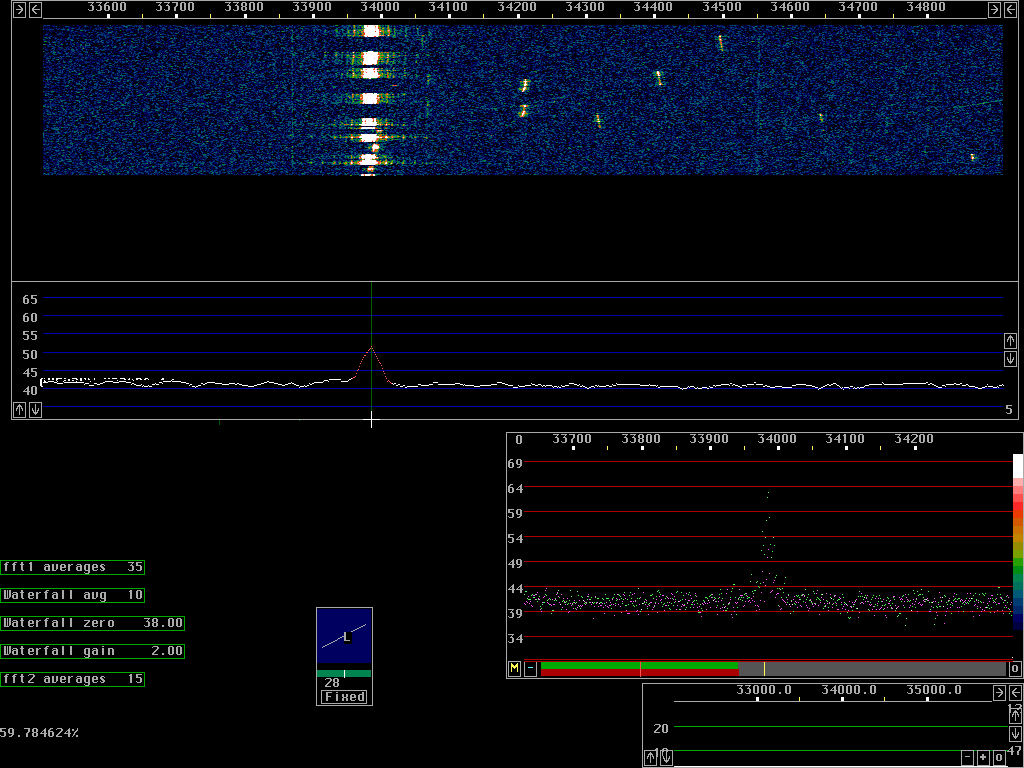
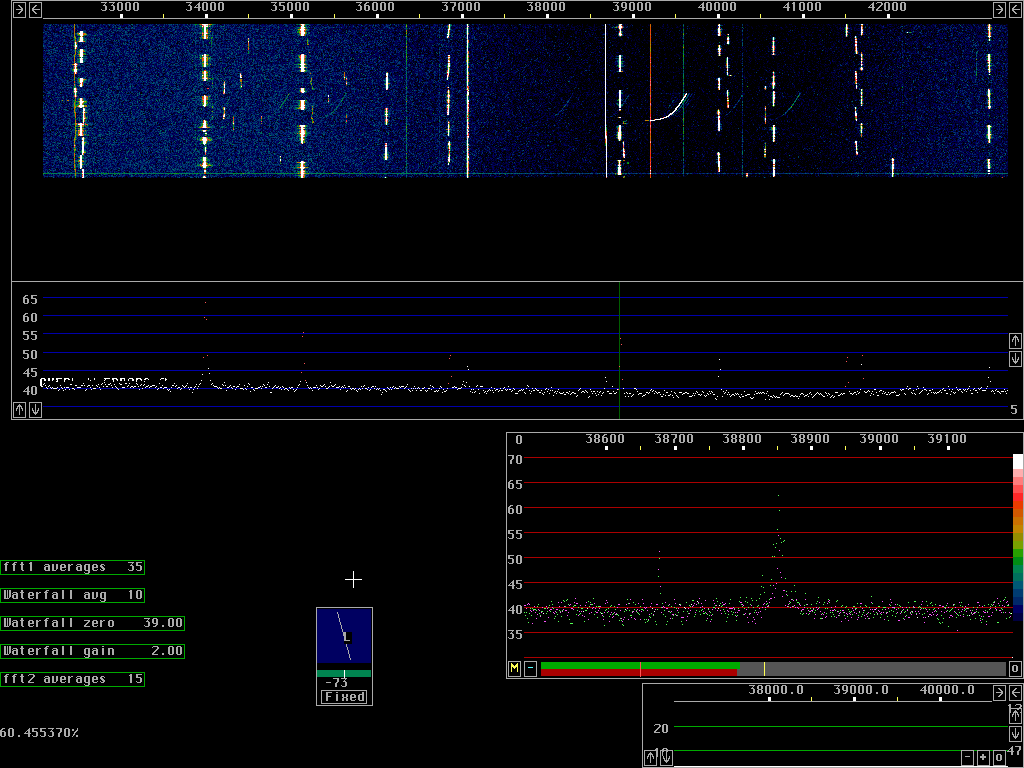
Figure 2 shows exactly the same sequence as fig. 1 but this time it shows the output from the second fft. The first fft is run with 8192 points while the second fft is run with 65536 points. Note that the sensitivity is much higher. The very weak signals at about 34kHz are easily visible now and several more signals are easily located.


Fig 2. High sensitivity waterfall power spectrum. Each pixel colour corresponds to the largest value out of the 64 power bins that span the frequency range between two pixels. 62% of the available CPU time is used.
When the second fft is enabled the fft output is is not only displayed in the form of a waterfall graph. If a frequency is selected by a mouse click on the wide graph - waterfall or spectrum - the high resolution graph shows the second fft spectrum in the currently selected polarisation with one green pixel for each fft bin. The orthogonal polarisation is shown with magenta dots.

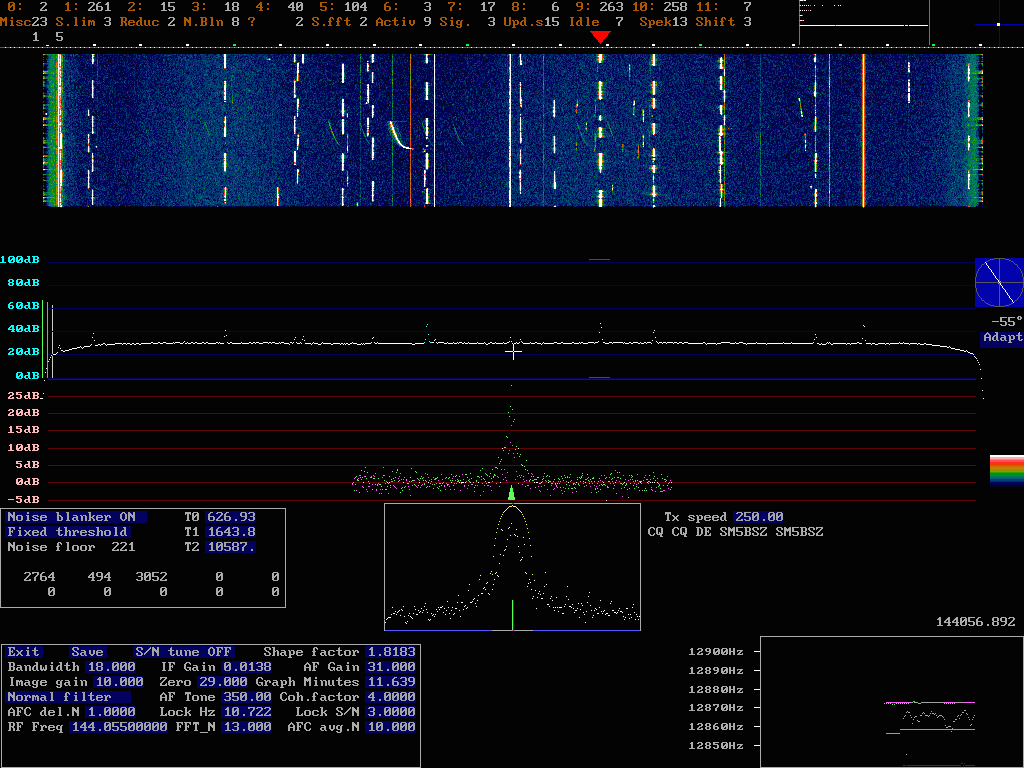
As a comparison fig. 3 shows how the same sequence looks on the old MSDOS system. A signal at frequency F kHz in fig. 2 is displayed also at 96-F kHz in fig 2. The corresponding frequency in fig. 3 is 48-F kHz.

The weak signals around 34kHz in fig. 2 show up around 14 kHz in fig.3. The red triangle on top of the frequency scale is at 12.85 kHz. The MSDOS system has proven to be sensitive enough to discover signals that are too weak to copy. The 90kHz waterfall graph of fig.2 is similar in detect performance although one has to look closer and use a good screen.


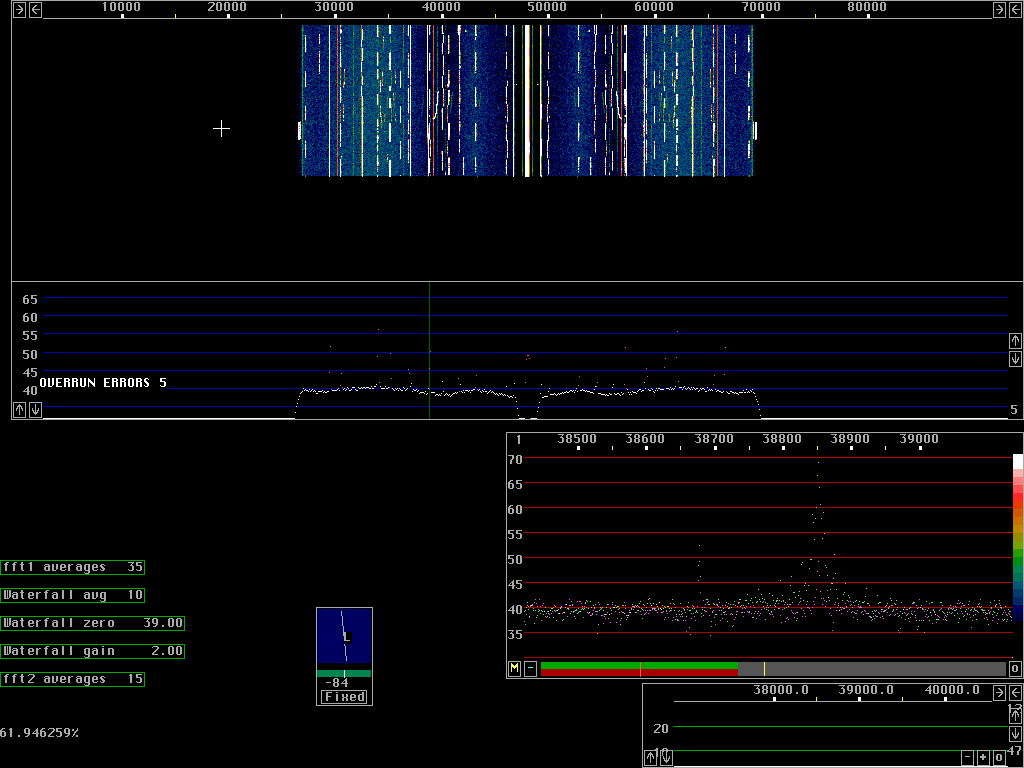
Fig 3. The MSDOS dsp display of the same sequence used for all the images on this page as a reference for detect sensitivity.
Contrary to the MSDOS system, Linux dsp is very flexible. If the frequency is known one can zoom and display a narrower frequency range over the screen. Fig. 4 shows a zoom by about 10 times. Zooming like this makes the signals easier to see but it does not really reveal anything new.

Fig 4. Zooming makes signals easier to see but in case there is still many power values behind each pixel the detect performance is not very different.
Figure 5 shows the region around 34 kHz zoomed to one pixel per point. Note that the noise floor is lower now by about 1dB (38 compared to 39 in the other graphs). This is because there is no picking of the strongest any more. The spur at 33870 which is clearly visible now can not really be discovered in any of the other images.


Fig 5. Zooming to one waterfall point per pixel gives a small improvement in sensitivity for the waterfall graph. The spur at 33870 is not visible in the spectrum which is averaged over 15 transforms (5 seconds). Each line in the waterfall graph is averaged over 10 transforms.