MEASURING NOISE FIGURES
Chuck MacCluer W8MQW 1/27/97
Excess noise ratio: To the input of this realworld amplifier
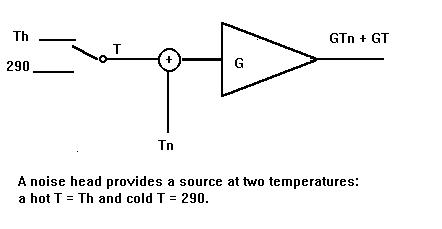
let us attach a `noise head,' a device that normally appears as a 50 Ohm load
(at T = 290 degrees) but, when a voltage is applied, a source at much higher
temperature T = Th.
The excess noise ratio (ENR) of the head is
ENR = (Th - 290)/290 = Th/290 - 1.
The excess noise is achieved by biasing a noisy diode. The ENR is stamped on the body of the noise head; a value of 15.5 dB is typical at 1 GHz. The voltage applied to the head is usually 28 Volts to switch on the hot source temperature of T = Th.
The Y factor: Let us now measure the ratio of power out from the amplifier from applying the cold T = 290, followed by applying the hot T = Th as inputs:
Y = G(Th + Tn)/G(290 + Tn)
= (Th/290 + Tn/290)/(1 + Tn/290),
the famous Y factor. This measurement is easily done by dialing in sufficient attenuation until the output from the hot source T = Th is reduced to the level of output from the cold input source T = 290. Read off the required attenuation (in dB), convert with antilogs to the ratio Y. This can be done automatically using op amps in summing, log, and antilog configurations.
In terms of the noise factor F: As discussed on the previous page,
F = Tn/290 + 1
is called the noise factor of the amplifier. Thus by substituting Tn/290 = F-1, the Y factor becomes
Y = (Th/290 + F - 1)/F = (ENR + F)/F = ENR/F + 1.
Summary: The noise factor, excess noise ratio, and Y factor are related by
F = ENR/(Y-1) .
Thus the noise figure f of the amplifier is
f = 10 log F = 10 log ENR - 10 log (Y-1),
and its noise temperature is
Tn = 290(F - 1).
Example: A noise head is calibrated to have an ENR of 15.6 dB at 1296 MHz. When the noise head is connected to the input of a 1296 LNA, we find that a 15.3 dB pad is required to attenuate the hot output down to its cold output. Thus the Y factor is
Y = 10^1.53 = 33.9 (corrected Sept 2013 by SM5BSZ. Was 34.1 )
This means the noise figure of the LNA is
f = 15.6 - 10 log 32.9 = 0.4 dB, (corrected Sept 2013. )
with noise factor
F = 10^0.04 = 1.0965, ** see below
and noise temperature
Tn = 290 (F - 1) = 290 (0.0965) = 28 degrees Kelvin.
** Comment added by SM5BSZ Sept 2013
The uncertainties in the Y factor are large. Firstly the typical
accuracy of noise head calibrations is 0.2 dB. The attenuator
is presumably uncertain by 0.1 dB but the actual attenuation
depends on the impedance matching at the point where it is inserted.
A 0.4 dB NF corresponds to Tn = 28 K, but the example is a measurement
that finds the NF to be in the range 0.1 to 0.7 dB or something of
that order with a noise temperature in the range 7 to 51 K.
The accurate measurement of low noise temperatures is non trivial.
Look at the links in the section Low noise amplifiers
on this page: SM5BSZ home page
